
Isn’t it time for a new kind of clock?One that shows us where the sun is!
Because the time our clocks give us is based on the position of the SUN as seen from Earth. Time is actually the earth’s rotation relative to the sun (not the stars).
This clock is an addition to the clocks we use now, not a replacement.
Because I use a celestial sphere (3D) to indicate where the stars are instead of a flat (2D) map, there are no differences as with the 2D view. As you can understand, this 3D view on the celestial sphere makes it possible to position this sphere so that all stars are aligned! That’s why I designed this frame (consisting of rings) to position the celestial sphere so that all the stars on it are aligned seen from the center of the celestial globe.

The celestial sphere in this clock is the only part of the clock that I did not produce/design myself. The frame around it that I designed is a tool to place the globe so that all the stars are aligned seen from the center of the celestial globe. Since our sun is also a star, it is also displayed on the celestial sphere, but our planet goes around this star (the sun), which means that we see the sun moving past the other stars in a circle called the ecliptic. To know where the sun is currently in space (among the other stars) you have to look at the date on the ecliptic. Putting the frame in place so that all stars are aligned is done in 5 steps. Entering the date and time are the last (easy) steps, the other steps you have to do 1 time if you do not move the clock itself. That’s why I use a motor to fill in the time and date, because time and date change all the time, while the data like latitude and longitude or the direction to the north remain the same if you don’t move the clock itself. Now you look at the date to see what time it is. But this date needs a pointer, otherwise you have to search for it to see the time immediately. This pointer I made goes around in 1 year and has 1460 (365 x 4) steps so every 6 hours adjustment is needed, to make this go automatically is my last challenge for this clock. This clock runs on a stepper motor (2048 steps per rotation (360 degrees), the power supply is mini-USB so 5 volts max 1 ampere = 5 watts max. The RTC (real time clock) is the one that gives the command to make a step. Or actually it takes 4 steps every 7 seconds and every 1019 seconds 1 step back to make the sphere rotate as slowly as the planet relative to the stars (not the sun). This is half a second a day too slow, if I used 1020 instead of 1019 it would run half a second too fast. (It should be one step per 1.753009734 seconds). To make the globe rotate smoothly I designed a kind of hub-less wheel, 12 ball bearings (6 on each side of the disc) (every 60 degrees) hold the ring / disc attached to the sphere at the equator in place so that it can rotate smoothly. This ring/disc has 720 teeth and on the outside (around 720 teeth) there are small gears every 60 degrees with 30 teeth each that hold the ring in place and 1 of the 6 gears is the stepper motor.

This product is not yet ready for sale. Yes, we call it a prototype. And yes, I can’t produce it all myself, so this is a call to create a partnership to make it sales-ready. The globe itself is not perfect, there are large holes in it at the north and south poles to put a light in it on its original stand and with this light in it, it will give the constellations as drawings of real animals, for example, the big bear is depicted as a big bear drawn over this constellation. This feature is not necessary for my clock but could be retained as long as the globe itself does not have big holes. The celestial spheres are no longer mass produced, I discovered, at least they are no longer for sale in my country or to be ordered on the internet. In the US they may still be selling the transparent spheres with the stars printed on the inside of the celestial sphere, this is the best way to display the stars now that they are not mirrored or upside down so this should be perfect you would think, but in this transparent sphere there is a small globe (in the middle of the big celestial sphere) but to find a star you have to be able to look through this center, so it’s not perfect either. And the precision of globes using plastic wrap with the stars printed on it and then taped to or into the globe is questionable. Then I would like to add something to the globe: the earth’s axis moves very slowly through space (1 round in about 26,000 years). This movement is the difference between a sidereal and tropical year, but the axis of the clock is attached to the globe and thus does not move. If this axis is attached to the celestial sphere at some point (36 years in the future) then you have less than half a degree difference. If someone knows exactly how to move the axis of the celestial sphere over the celestial sphere itself, that would be the solution to make it count tropical years instead of sidereal years that I am now using as a solution. So I made it active for 72 years. From this year to 72 years in the future. The years to use are the years that are divisible by 2 and not by 4, so years right between the leap years. You could use it longer than that or go back in time, but the difference in that case will be more than half a degree. If you think you can move the axis very easily through the circle of precession (the one that goes around in 26,000 years) for hundreds of years, keep in mind that the sphere is attached to the equator. Do you see what I mean?
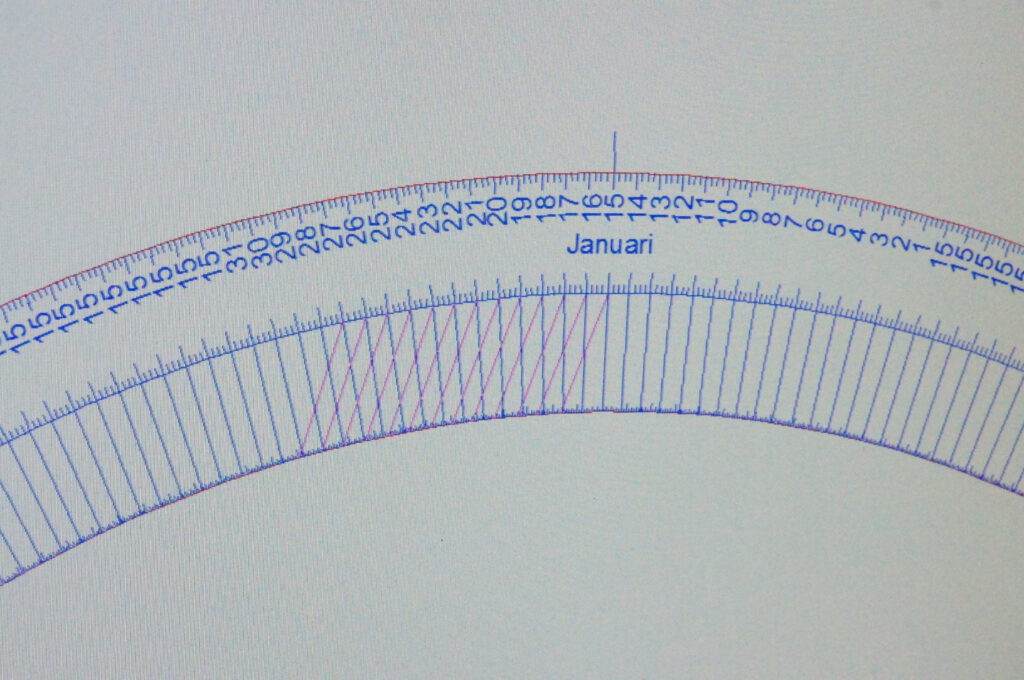
The time-rings are situated parallel to the equator (perpendicular to the axis of the earth) in this clock because the laws of time that are made in Greenwich say so. Equation of time does the same: there are two equations: 1 the elliptic path of the earth around the sun that causes differences through the year: there where the earth is closest to the sun the angles are a bit greater than 1/365 of a circle while there where the earth is farthest from the sun the angles are a bit smaller than 1/365 of a circle. 2 is far more difficult to see but let me describe it as a projection from the axes towards the equator passing by the ecliptic when you do so it will give angles bigger than 1/365 of a circle at the solstices (both of them) and smaller than 1/365 of a circle at the equinoxes (also both). Equation of time number 2 makes the 8 shaped analemma, and thus 4 points in the year where equation of time is zero. These 4 zero points are the points where the globe is attached to the datum-ring with paws that go radial. So there are only 4 dates in the year where the paws are radial, the other 361 are not radial. There are 2 dates in the year that have maximum difference: February 11th and November third. These two dates have paws in my design, paws that are not radial but (most) oblique. Some of my clocks have 8 paws: 6 as just described and two extra because there are smaller differences in the year but still they are maximum oblique in their surroundings. So now you think that 365 – 8 = 357 dates have no paw? That’s correct but I designed a disc (transparent) with 365 stripes on it, 4 of them are radial, 2 of them are big max and two small max and 357 are also differences (not radial). Why did I designe it like this? Because now the 365 stripes are the difference between local mean time and true sun time. Follow the stripe on the date of today and you see the true sun time on the outer time-ring while if you go radial you see the local mean time on the outer time-ring, (the inner time-ring is for the clock-time)…
